Comprendre le principe de l'analyseur de spectre est fondamental pour les ingénieurs RF, les concepteurs de systèmes et les professionnels du test et de la mesure. Un analyseur de spectre convertit les signaux du domaine temporel en signaux du domaine fréquentiel, ce qui permet aux ingénieurs d'évaluer la largeur de bande du signal, les émissions parasites, le bruit de phase, les harmoniques et les interférences.
Les analyseurs de spectre modernes reposent principalement sur deux architectures distinctes : les analyseurs de spectre à accord par balayage et les analyseurs de spectre basés sur la transformée de Fourier rapide (FFT). Bien que les deux visent à afficher la puissance du signal en fonction de la fréquence, leurs mécanismes internes, les compromis de performance et l'adéquation de l'application diffèrent considérablement.
Cet article analyse ces deux approches du point de vue d'un ingénieur en R&D, en incorporant des fondements mathématiques, des considérations au niveau du système et des références à des publications internationales faisant autorité.
Principes de base de l'analyseur de spectre
Le principe de base de l'analyseur de spectre consiste à transformer un signal du domaine temporel au domaine fréquentiel. La transformée de Fourier continue est définie comme suit :
X(f)=∫-∞∞x(t)e-j2πftdt
Cette équation exprime la manière dont un signal dans le domaine temporel (x(t)) est décomposé en ses composantes de fréquence. Les analyseurs de spectre pratiques mettent en œuvre cette transformation soit par balayage de fréquence à l'aide de matériel analogique, soit par échantillonnage numérique suivi d'un calcul FFT.
Le choix de l'implémentation affecte directement la résolution de fréquence, la gamme dynamique, la vitesse de mesure et la capacité à capturer les signaux transitoires.
Principe de l'analyseur de spectre syntonisé par balayage
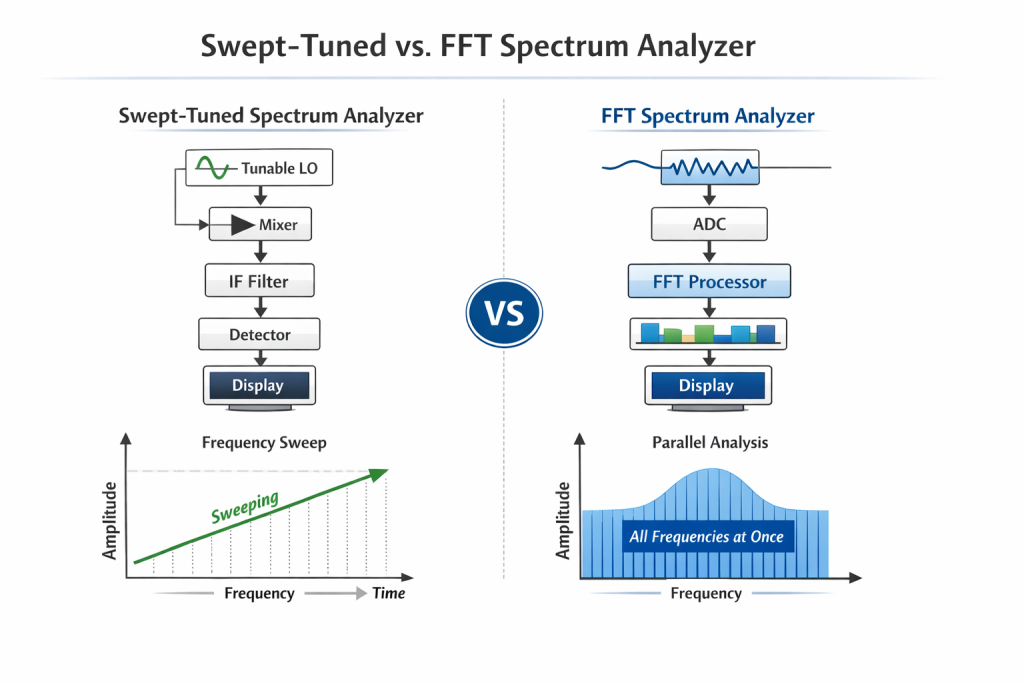
Architecture superhétérodyne
L'analyseur de spectre à accord par balayage est la conception traditionnelle et historiquement dominante. Il est basé sur l'architecture d'un récepteur superhétérodyne, largement utilisé dans les systèmes de communication RF. L'analyseur balaie séquentiellement une gamme de fréquences définie à l'aide d'un oscillateur local (OL) accordable.
La chaîne de traitement du signal se compose généralement des éléments suivants
- Atténuation d'entrée et filtrage de présélection
- Baisse de fréquence via un mélangeur
- Filtrage fixe de la fréquence intermédiaire (FI)
- Détection de l'enveloppe et amplification logarithmique
- Balayage et affichage synchronisés de la fréquence
Lorsque l'OL balaie les fréquences, seuls les signaux situés dans la largeur de bande du filtre FI sont détectés à chaque instant, formant ainsi un spectre complet au fil du temps.
Le principe de l'analyseur de spectre à balayage est mathématiquement analogue à un filtre à bande étroite glissant sur l'axe des fréquences, mesurant la puissance du signal point par point [1].
Points forts et limites
Les analyseurs de spectre à syntonisation par balayage offrent :
- Large couverture de fréquences (du kHz aux ondes millimétriques)
- Gamme dynamique élevée et excellente sensibilité
- Architecture matérielle mature avec étalonnage stable
Cependant, ils présentent des limites inhérentes :
- Incapacité à capturer des signaux de courte durée ou transitoires
- Possibilité de manquer des interférences intermittentes
- Le temps de balayage augmente avec la largeur de bande de la résolution et la portée.
Ces limitations deviennent critiques dans les systèmes modernes impliquant des sauts de fréquence, des transmissions en rafale ou des environnements spectraux denses [2].
Principe de l'analyseur de spectre FFT
Échantillonnage numérique et traitement FFT
Le principe de l'analyseur de spectre FFT repose sur conversion analogique-numérique (ADC) à grande vitesse suivi d'un traitement numérique du signal. Le signal d'entrée est échantillonné à un taux satisfaisant le critère de Nyquist :
fs≥2B
où (fs) est la fréquence d'échantillonnage et (B) la largeur de bande du signal.
Un bloc de (N) échantillons du domaine temporel est ensuite traité à l'aide de la transformée de Fourier discrète (DFT), calculée efficacement via l'algorithme FFT :
X(k)=n=0∑N-1x(n)e-j2πkn/N
Cette approche calcule l'ensemble du spectre de fréquences simultanément plutôt que séquentiellement [3].
Fenêtrage et fuites spectrales
Dans les analyseurs de spectre FFT du monde réel, les fonctions de fenêtre (par exemple, Hanning, Blackman-Harris) sont appliquées pour atténuer les fuites spectrales causées par les enregistrements à temps fini. La sélection des fenêtres influence directement la précision de l'amplitude et la résolution de la fréquence, ce qui est important pour les mesures de précision.
Analyseur de spectre Swept-Tuned vs. FFT : Comparaison technique
Compromis de performance
| Paramètres | Analyseur de spectre syntonisé par balayage | Analyseur de spectre FFT |
| Acquisition de fréquences | Balayage séquentiel | Traitement parallèle |
| Capture des signaux transitoires | Limitée | Excellent |
| Gamme dynamique | Très élevé | Limité par l'ADC |
| Vitesse de mesure | En fonction du balayage | Quasi instantané |
| Complexité | Analogique à forte intensité de RF | Numérique à forte intensité de DSP |
Du point de vue du principe de l'analyseur de spectre, les modèles à accord par balayage excellent dans l'analyse de signaux stables et continus, tandis que les modèles basés sur la FFT dominent les applications nécessitant une connaissance du spectre en temps réel [4].
Analyse du spectre en temps réel et architectures hybrides
Les analyseurs de spectre modernes en temps réel intègrent des FFT qui se chevauchent, des mémoires tampons profondes et un traitement basé sur le FPGA pour éliminer le temps mort. Ces instruments garantissent une probabilité d'interception (POI) pour les signaux dépassant une durée et une amplitude spécifiées.
Pour remédier aux limitations de la couverture de fréquence, de nombreux instruments haut de gamme utilisent des architectures hybrides, combinant des frontaux accordés par balayage avec un traitement FI numérique basé sur la FFT. Cette conception associe une large gamme de fréquences à une capacité de détection en temps réel, ce qui reflète les tendances actuelles de l'industrie [5].
Considérations relatives aux applications techniques
Du point de vue de la R&D, le choix d'une architecture d'analyseur de spectre dépend des exigences de l'application :
- Essais de conformité EMI/EMC privilégie souvent les analyseurs à balayage pour leur gamme dynamique.
- Développement de protocoles sans fil et chasse aux interférences bénéficier des principes de la FFT et de l'analyseur de spectre en temps réel.
- Analyse avancée de la modulation nécessite généralement un traitement numérique basé sur la FFT.
Comprendre le principe sous-jacent de l'analyseur de spectre permet aux ingénieurs d'interpréter correctement les mesures et d'éviter les erreurs de diagnostic dues aux limites de l'instrument.
Conclusion
Le principe de l'analyseur de spectre est mis en œuvre par le biais de deux méthodologies fondamentalement différentes : le balayage de fréquence à accord balayé et l'analyse de spectre numérique basée sur la FFT. Les analyseurs à accord balayé reposent sur des architectures superhétérodynes et des mesures séquentielles, tandis que les analyseurs FFT utilisent un échantillonnage à grande vitesse et un calcul de fréquence parallèle.
Chaque approche présente des avantages et des contraintes uniques. Les systèmes RF devenant de plus en plus complexes et dynamiques, les analyseurs de spectre hybrides et à base de FFT sont de plus en plus essentiels. Toutefois, les analyseurs à balayage restent indispensables pour les mesures à large bande et à gamme dynamique élevée.
Une bonne connaissance de ces principes est essentielle pour les ingénieurs RF chargés de la conception, du débogage et de la validation des systèmes.